활성화 함수가 왜 필요한가?
에 관해서 완전 자세히 초등학생도 이해할 정도로 풀어보자.
우선, 퍼셉트론의 구조에 관해서 살펴보자.

위에 구조에서 살펴볼 수 있듯이,
1. 입력값에 가중치(특징)을 곱한다.
2. 하나의 출력으로 나타낸다.
3. 활성화 함수를 거쳐서 또 다른 값으로 나타낸다.
그리고 책과 블로그 등에서 하는 말에 관해서 살펴보자.

위에 말을 들으면 뭔가 고개가 끄덕여진다.
만일 은닉층을 여러 개 둘 경우, 선형 함수의 값을 다음 층의 입력값으로 넣으면
선형함수(선형함수(...)) 이러한 형태가 되니까,
결국에는 선형이므로 층이 의미가 없어지는 것처럼 느껴진다.
하지만 그렇다면,
활성화 함수를 넣으면 왜 의미가 생기는 것일까?
선형 함수의 중복은 의미가 없다는 건 쉽게 상상이 가지만,
활성화 함수가 의미 있다는 것은 나로선 쉽게 상상이 가지 않는다.
활성화 함수가 없으면,
층이 깊어져도 결국 선형 함수인 것을 부정했으니까,
반대로 활성화 함수를 넣으면 층이 깊어지면서 비선형 함수가 된다는 걸 알 수 있다.
즉, 활성화 함수가 있으면,
처음엔 선형 함수로 시작하더라도
결국 값은 비선형 함수가 된다는 걸 의미한다.
그럼 여기서 질문.
어떻게 활성화 함수로 인해 비선형 함수가 될까?
그리고
왜 우리는 비선형 함수가 좋다고 가정하는 걸까?
우선 결론부터 말하자면, 대표적인 문제인 XOR 문제를 풀 수 있게 되고,

이로 인해, 선형으로는 못 하던 복잡한 분류가 가능해진다.
그리고 더 나아가,
우리가 접하는 대부분의 데이터
예를 들면 이미지, 음성, 텍스트 같은 것들
이런 것들은 거의 다 비선형적인 구조를 가지고 있다.
그래서
이 문제를 해결하는 첫 번째 스텝이 바로 "비선형 함수"를 만드는 것이라고 생각한다.
이것이 나의 생각이다.
그럼, 왜 활성화 함수를 넣으면 왜 의미가 생기는 가
* 예시로 이해 (왜 비선형 없으면 안 되는가):
선형만 쌓으면:

→ 사실 이거 다 합치면:

→ 결국 그냥 하나의 affine 변환 (선형 변환 + 이동).
→ 아무리 층을 많이 쌓아도 하나의 직선 / 평면 / 선형 함수밖에 안 됨 ❌.
ReLU (혹은 다른 비선형) 있으면?

→ 이러면 중간중간 꺾임이 생기니까 →
→ 복잡한 곡선 / 휘어진 경계 / 여러 조각으로 나눠서 표현 가능.
+) 추가 설명: ReLU함수란?
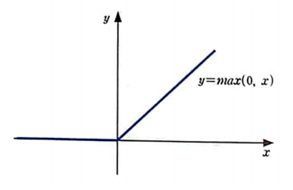
위 그림과 같이 0을 기준으로
* 음수값은 아예 삭제
* 양수값은 살리는 함수이다.
다시 본문으로 돌아와서,
=> 왜 저게 중간에 꺾임이 생기가 하는가?
ReLU를 중간에 넣었을 때 (Affine → ReLU → Affine)

수식 흐름 (1D 예시로 쉽게):

결과:

=> 직선이 하나로 이어진 게 아니라, 꺾여서 두 구간으로 나눠짐
+) ReLU 없는 경우
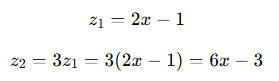
시각화

=> 이렇게 꺾이는 직선을 표현할 수 있어서 XOR문제를 풀 수 있게 되는 것이다.
=> 깊이가 많을수록 꺾임을 "다양하게 조합" 가능하지만, 무조건 층 수와 일치하지는 않음

추가적으로, 3번 꺾이는 과정을 보여주자면

시각화

결론
"XOR은 다층 퍼셉트론이 필요한 이유를 보여주는 예시고,
다층 퍼셉트론을 가능하게 해주는 게 바로 활성화 함수다.“